前言

昨天我們說明了馬可夫鏈，並了解馬可夫鏈會收斂的條件與過程，今天我們要正式進入與強化學習有關的馬可夫決策過程。

馬可夫決策過程

和馬可夫鏈比起來，馬可夫決策過程有一個很明顯的差異，轉移的過程不再是依照轉移矩陣，有一個固定的轉移機率，而是按照處於的狀態與動作決定。數學家是這麼定義的：

• 狀態集 (Set of states)：所有可能的狀態，記為
• 初始狀態 (Initial state)：
• 動作集 (Set of actions)：所有可能的動作，記為
• 轉移模型 (Transition model)：轉移到下一個狀態的模型，記為
• 獎勵函數 (Reward function)：評價「決策的結果是好、或不好」的函數，記為

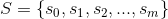
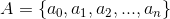
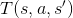
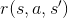
在馬可夫鏈中，我們已經與第 1, 2, 4 點打過招呼，現在我們先解釋動作集的內容。

動作集

動作集與狀態集有相似的地方，都記錄著所有可以執行的動作，在每個狀態下，雖然可能會有幾個比較好的動作，但還是可以執行所有的動作。(ex: 過年跟長輩拿紅包的時候，要跟長輩說吉祥話，但你也可以跟長輩說 你吃飽沒)

可以執行所有動作這件事，在馬可夫決策過程中很重要。還記得 Day3 中提到收斂條件嗎？這件事確保任意狀態可以轉移到其他狀態。

我們回想小明的例子，假設小明在躺著 () 與坐著 () 的時候，會執行看漫畫 () 與讀書 () 兩件事。那麼我們可以用條件機率的方式，表達一些事情：

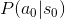• 表示小明躺著的時候，看漫畫的機率。
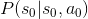• 表示原本小明躺著看漫畫，下一時刻還是躺著的機率。

獎勵函數

我們回到小明的例子，例子中的狀態集與動作集，可能的狀態與動作都很少。如果我們今天在一個很複雜的狀態，可以採取很多動作的時候，就不可能一個一個去判斷要什麼狀態要採取麼動作。因此，數學家設計一個稱為 agent (代理人) 的概念，自動判斷什麼狀態要採取什麼動作。

不過不同的代理人，可能對事情有不同的作法 (別說是代理人，不同人對事情都有可能有不同的作法) 。數學家認為，有不同的作法，是因為解決事情的 策略 不同。以小明的例子而言，當乖小孩可能是一個策略，所以會一直保持坐著、看書，這樣的狀態與動作；讓自己近視可能是一個策略，所以會一直躺著看書、看漫畫。因此我們需要一個標準、評分方式，來調整我們的策略，而那個評分方式就是獎勵函數。

整體而言

我們的代理人，根據採取的策略，會在不同狀態下決定要採取動作，並在動作後會得到回饋，調整現在的策略。如果你接受這個流程的話，那麼你還有一個問題要解決。

回饋怎麼影響代理人的策略？這個時候你需要一個「價值函數」，評估目前可以轉移的狀態的價值。